Improving the
Gateway Math Class Pass Rate
With Supplemental
Instruction
The only mathematics course
with no prerequisites currently offered at a mid-sized southwestern urban open-admissions
university with a diverse population (Downtown University1, 2005; U.
S. News & World Report, 2000), is here called Algebra Tutorial. This foundations (i.e. developmental, remedial, or
college preparatory) course is a prerequisite for college-level mathematics
work. A student places into this course with a score below 63 on the
mathematics questions in Accuplacer, below 500 on the SAT in mathematics, or
equivalent (Downtown University, 1999; National Evaluation Systems, 2003). With
"fewer than half of high school graduates … prepared for
college-level math" (Redden, 2006), Algebra Tutorial mirrors courses
offered at many other institutions.
Course Description
Algebra Tutorial begins
with a study of natural, whole, integer, rational, and some irrational forms of
real numbers. One main focus for this course is that students become proficient
at solving progressively more complicated linear equations although some work
on two-sided and three-sided linear inequalities is included. An introduction
to two- dimensional graphing with an emphasis on graphing linear equations is used
to lay a foundation for graphing systems of equations and inequalities in the
second foundations course. Polynomial
________________________________________________________________
1The
name Downtown University has been assigned as a
pseudonym for the purpose of this paper.
calculation
addition, subtraction, multiplication, and division by a monomial is included.
The course ends with an introduction to factoring common monomials from polynomials
and this topic is where the second course begins.
The department syllabus
specifies the required textbook, the sections of material that must be included, the mastery values that should be assigned on
the PLATO (2000) modules, suggests amount of time to be allotted to each
chapter, and states that there should be three or four tests. Yearly, a faculty
committee develops a student syllabus, student final exam review sheet and the
different versions of the required, comprehensive, multiple-choice, 50 question
final exam (Downtown
University, 2003b). The
final exam review sheet is available to students near the end of the semester
in hardcopy form from the copy center on campus or from a department web site.
This paper asks the following questions: How has the foundations program
Algebra Tutorial course evolved in recent years, how effective has it been,
what is the percentage of students successful in different semesters as we
change the policies governing the class, and why is one of the greatest
determiners of student success whether or not a section has a Supplemental
Instruction leader?
In a typical
fall semester there are about 30 course sections with about 30 students and one
faculty member per section. The spring semesters have always had a lighter
enrollment (See Table 1.). Up to 10% of the instructors for Algebra Tutorial are
tenured or tenure-track faculty, approximately 50% are adjunct, and the
remaining are lecturers (Author, 1999, 2001). Each instructor follows the
department syllabus (Downtown
University, 2003a) but
decides the style and format of the class sessions. Algebra tutorial students
work in class with a faculty member three class hours per week. Some students
elect to take this course because of their lack of confidence or their
perceived lack of skill in mathematics so they want to take the first course.
Most students take this non-degree, three-credit course because they did not
score high enough to place out of it when they took the placement test.
Milieu
Nationally, about 75% of
developmental students successfully complete their remedial courses (Lewis,
Farris, & Greene, 1997; Mansfield, Farris, & Black, 1991). However,
this rate only refers to passing. It does not specify how many semesters are
involved. The time and effort it takes a particular student to pass a course
will vary depending on the amount of remediation needed and other factors
pertinent to that individual. Though the Downtown University
semester pass rate has changed and has even increased (See Table 2.), the
reasons or processes causing change are not obvious. If we knew why or how it
is changing, then such insight would be used to foster more improvement in
order to reach the 60% goal for the past rate called for by the university's
administration (K. Oberhoff, personal communication, January 1999).
In the current education
milieu, there are individuals and organizations in the United States with opinions on the
current state of education who desire to affect change. Standards set by
accrediting agencies and state legislative mandates are the main driving forces
for new policies and procedures. Locally, there is increased demand for
accountability felt from the top down by the university administration, the
department, and the faculty. The simple directive of improving the pass rate of
Algebra Tutorial is as a local example of a legislated attempt to improve
education by mandate. The suspected root causes of the pass rate problem mirror
problems in the general American population.
Some of the socio-economic
factors present in high-poverty schools (Kannapel, Clements, Taylor, &
Hibpshman, 2005a, b; Viadero, 2005) repeat themselves in the lives of Algebra
Tutorial students at Downtown
University. The legacy of
similar socio-economic factors include the following: (a) many are members of
minority groups, (b) many have scored at the lower of the academic-achievement
scale, (c) some have possibly been just passed along in previous courses, (d)
many may have attended schools that had minimal resources, a high turn-over
teacher population, and teachers assigned to courses out of their area of
expertise, and (e) many have families with health and welfare difficulties. The
above characteristics of high-poverty schools are also known to be some of the
characteristics of low-performing schools (Betts, Zau, & Rice, 2003;
Greenwald, Hedges, & Laine, 1996; Kannapel, et al., 2005b).
Algebra Tutorial Data
The construct from
the second question concerns why Algebra Tutorial students are successful. Even
if we define successful as earning an A, B, or C in the course, the reasons for
not receiving an IP, F, or W cannot be observed directly. Some known reasons
for a student not passing are: (a) the in progress grade IP is given to
students who achieved less than the required 70% average but the teacher has
documented evidence of their good effort and work; (b) the failing grade of F
is assigned to students who miss more than 6 hours of class or did not meet the
minimal faculty expectations. It is assumed that the unknown reasons can also
be quite different for earning the different non-passing letter grades. The
crux of the problem is that there are many unknown factors affecting the grades
a student receives in a course and finding out exactly what all the factors are
or the strength of any factor's importance has not yet been achieved.
Hopefully, a successful
remediation program can be designed for Downtown University.
Unfortunately, a successful program achieved by following best practices found
at other universities is only a process-product approach (Berliner, 1990;
Greenberg, 1999; Kinach, 1995; Orton, 1998) which has, thus far, been
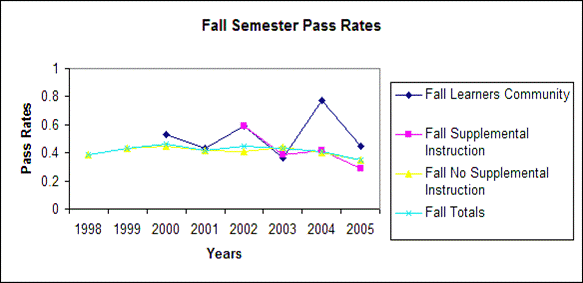
insufficient for meeting the mandated 60% pass rate. But Figure 1, based on
Table 3, indicates that improvement can be made. There were 356 passing
students out of 924 enrolled students in the Fall 1998 semester for a 39% pass
rate. With many innovations and changes in the course, new results show
improvement in the pass rate. In the Fall 2004 semester, there were 352 passing
students out of 855 students enrolled in Algebra Tutorial for a 41% pass rate.
The lower enrollment was probably due to many factors including the fact that
the Legislature cut funding to higher education to "avoid a general
increase in state taxes during a 2003 budget crunch" (Robison, 2006) and
tuition increased.
There is documentation that
63% of Algebra Tutorial students pass when taking the course for the first
time, 40% of those who retake the course pass on the second or third attempt,
and very few students actually repeat the course more than once (Waller, 2003,
2005). With the implementation of
various initiatives and accounting systems, the pass rate has improved. The
evolution of the course has been the result of a concerted effort in the
department responsible for teaching the course. A great deal of time and
reflection on the part of individuals, along with expansion of professional
knowledge by many faculty members of all ranks and serving on various
committees, continues to contribute to the effort.
Recently, an attendance
policy was instituted for Algebra Tutorial and it has now been extended to the
other mathematics foundations course at Downtown University.
Though St. Clair (1999) can argue that compulsory attendance policies do not
improve academic achievement in general, they can be useful in showing
foundations students that attendance is helpful for success in college courses
(Finder, 2006; Gardner, Barefoot, & Swing, 2001). While attendance policies
try to force students to attend, it is the content, teaching practices, and
design of the classes that will make worthwhile learning experiences that the
students see as beneficial so that they are willing to attend classes. Motivating
students is a very difficult, elusive to many, but important aspect of
foundations teaching. One way to make courses more interesting and student-friendly
is to integrate class and laboratory work (Boylan & Saxon, 2000).
Integration of classes with individual laboratory work on PLATO (2000) and also
with group exercises has recently been incorporated into the Algebra Tutorial
course (Waller, 2002). Although detailed data showing what improvements to the
pass rate have resulted from incorporating laboratory and group work is not
individually and directly available, the indirect evidence is the increase in
the pass rates (See Table 2.) after the group exercises were designed and made
available in the department.
While there are other
learning community models (Henscheid, 2004; Love & Tokuno, 1999), a tutoring
program is one of the ways to bolster instruction with social support. Supplemental
Instruction is a common feature in learning communities. A history and details describing
SI is given below.
A Short History of Supplemental Instruction (SI)
Supplemental
Instruction (SI) began in the early 1970s with a pilot program in the School of Dentistry at the University of
Missouri-Kansas City (Arendale, 1998; Widmar, 1994). When the University of Kansas City
changed, from a small private institution serving the top 20% of high school
graduates to one with a more culturally and academically diverse population as
the University of Missouri-Kansas City, the entering student attrition rate
increased from 20% to an alarming 45%. Widmar includes further details about
the start of SI, but this description indicates a similarity in student needs between
our two universities.
Supplemental Instruction has spread to many other campuses because it has been
very successful in supporting (a) cultural diversity, (b) critical thinking, and
(c) retention and performance, while being replicable and adaptable (Widmar,
1994). It has documented effects on student leaders and faculty as well as on
students in a variety of programs. As a peer assisted learning strategy, it is
one of the two available research report topics at the United States Department
of Education's "What Works Clearinghouse" (Viadero, 2004). SI has
been included with reading and freshman orientation seminars. A typical
description of Supplemental Instruction was offered in Davidson and Hanson
(2000):
Supplemental Instruction (SI) is an academic support program that
utilizes peer-assisted study sessions. SI targets
historically challenging
academic courses and offers to all enrolled
students regularly scheduled,
out-of-class review sessions. Study sessions are
informal seminars in
which students compare notes, discuss readings,
develop organizational
skills, and predict test items.
The SI sessions are directed by student leaders, usually students
who have previously taken the course and passed
with at least a grade of
“B” and who audit the class during
the semester for which they are leading
the SI session. Many of our SI leaders are
recommended by faculty
members who have a first-hand experience of their
academic success.
(p. 1)
The
Learning Communities models with Supplemental Instruction (SI) have outstanding
examples of successful programs (Martin & Arendale, 1994). In fact, SI has
been designated as an “Exemplary Educational Program” by the United
States Department of Education (Davidson & Hanson, 2000). Elsewhere, as
well as at Downtown
University, SI was
designed to satisfy student, administrator, and faculty requirements for (a)
avoiding a remedial image,
(b) being
cost effective, (c) increasing retention, (d) maintaining high academic
standards, and (e) promoting independent learning.
Description of SI
Supplemental Instruction (SI)
has many of the features desired by foundations students. SI avoids a remedial
image in the eyes of the students because when it is introduced to a new class
of students it is described as having the prestige of having been developed for
a medical school, which in itself is obviously not remedial in a traditional
sense, and because it supports high-risk (pass rate less than 70%) courses
rather than high-risk students (Arendale, 1998; Martin & Blanc, 1994;
Widmar, 1994). SI is better than just having remedial courses because it is an
organized, systematic, and comprehensive program (Boylan, 1999; Widmar, 1994). The
SI model has a theoretical base in cognitive psychology, especially the metacognition
construct, because it teaches effective use of learning strategies (Kenney
& Kallison, 1994).
Another advantage of
Supplemental Instruction (SI) is that it is proactive by inviting students to
participate from the first day of class (Arendale, 1994). It is not reactive to
anything negative and it does not wait until its services are
“needed.” Its voluntary attendance policy gives an aura of being
non-remedial (St. Clair, 1999). Being inclusive is another aspect of SI that is
seen as non-remedial. Everyone is welcome to the study sessions led by the SI
leader immediately, optimally, after each class (Arendale, 1998; Burmeister et
al., 1994; Higbee & Dwinell, 1998). Study sessions have advantages for
every student at any level. Findings from research studies in Kenney and
Kallison (1994) indicate that SI can help lower ability students significantly
increase their course achievement, and it can decrease study time for high
ability students. Usually, better prepared students tend to be attracted first
and this latter attracts less prepared students who are not normally likely to
admit to needing assistance (Arendale, 1994).
Maintaining high academic
standards is a requirement from the faculty so that students have a strong and
worthwhile course of studies. Programs that insure the consistency between exit
standards for remedial courses with the entry standards for college level
courses succeed in maintaining high standards (Boylan & Saxon, 2000).
Supplemental Instruction helps a university maintain high academic standards by
helping students achieve mastery of the subject at the level expected by the
professors (Arendale, 1998). In particular, course and oversight committees
align programs at Downtown
University.
Supplemental Instruction also
promotes independent learning by having students work with others in small
groups on how to learn as well as on what to learn (Arendale, 1998). The use of
active and collaborative learning strategies is one of the strengths of using
work groups (Arendale, 1994; Burmeister, et al., 1994; Good, Mulryan, &
McCaslin, 1992; Higbee & Dwinell, 1998; Kenney & Kallison, 1994).
Learning through SI allows students the freedom to try new skills for dealing
with coursework, empowers students to predict exam questions, may stimulate
higher-order thinking, and can make learning more meaningful. For example,
problem-solving skills are developed in general as well as in the specific
course content (Ainsworth, Garnett, Phelps, Shannon, & Ripperger-Suhler,
1994).
Regular discussions with an
SI leader incorporate glossary development and continue gradual learning
(Ainsworth et al., 1994). This is applicable to courses with a lot of new
vocabulary and reading. While many mathematics courses are not thought of as
reading intensive, developmental mathematics requires students to learn much
new vocabulary and notation. Mathematics is a foreign language to many students
so language acquisition skills are needed. Further, with 60% concurrently
enrolled in Reading (Author, 2005), Algebra Tutorial students have similar
characteristics to the population of students with mathematics plus reading
difficulties reported by Gersten, Jordan, and Flojo (2005). These students are
not able to verbalize their lack of understanding and need additional time to
develop fluency in performing computations. In SI, students are encouraged and
trained by the SI leaders to accept responsibility for developing many skills
(Ainsworth et al., 1994; Good, et al., 1992). Therefore, with the development
of their skills, all students can become more-independent learners.
Most students who need help
to pass a course would not be willing to increase their workload (Ainsworth et
al., 1994; Arendale 1994, 1998). However, learning how to be more successful
and efficient in study and work habits is desirable for all students. Since the
student bears no additional costs for tutoring, they do not fear or incur a
negative financial impact for using SI resources.
Supplemental Instruction
increases retention by integrating students into the social as well as the
academic university environment (Arendale, 1998; Boylan, 1999; Boylan &
Saxon, 2000; Good et al., 1992; Kenney & Kallison, 1994; Tinto &
Riemer, 2000). When students meet others with similar interests in the small group
SI sessions they often bond together. Peer study-groups help mainstream
disadvantaged students and culturally diverse students because of the mutually
supportive atmosphere (Arendale, 1994; Burmeister et al., 1994). Facilitating
resilience and encouraging at-risk youths with reasons to persist is important to
their academic success (Rockwell, 2006; Thielemann, 1999). Friendships begun in
SI sessions are springboards for students to sign up for future courses and
continue their education.
At Downtown University
the Supplemental Instruction leaders are students who are paid to attend the
regular classes as well as for their time leading discussion groups and
tutoring sessions outside of class. SI leaders need thorough training in SI
techniques and session routine (Ainsworth et al., 1994; Boylan & Saxon,
2000). Additionally, a review of foundations material strengthens the SI's
knowledge about the course concepts and keeps the material fresh for their use
in higher-level courses. The training can enlighten the leader and give new
insights leading to their own better study skills and improved work habits
(Ainsworth et al., 1994; Rishel, 1999). The position of leader has the added
benefit of increasing self-esteem because of their ability to share their knowledge
with other students and their faculty-like status. Major benefits for SI
leaders that were reported to the Downtown Learners Community include (a)
leaders excel in their own studies, (b) achieve self-confidence in their
academic and leadership skills, (c) establish rapport with professors, and (d)
acquire letters of recommendation for graduate school or future occupations
(Judge, 2006).
SI programs create
communities of learners that contribute to the life of the general society in a
way compatible to the fundamental aim of education "to enable individuals
to continue their education" (Dewey, 1916). Society, and hopefully the
students themselves will come to agree, it is worth their time and effort to
learn the skills that enable them to become successful college students when
the alternative is for them to never complete college (Boylan, 1999; Beneman
& Haarlow, 2002).
Note that while all
students must learn skills for independent learning, it is very important that
such skills be specifically taught to foundations students since, as has been discussed
earlier, it is the very lack of such skills that makes remediation necessary
for them. However, despite all the different approaches, philosophies, and
efforts used to develop exemplary retention strategies and programs, we must
not neglect the most important component – the students' perspective. It
is each individual student who personally decides whether or not to persist in a
course. Discouragement can and must be prevented for any program to be successful.
Students who are engaged, motivated, and willing to work are more likely to
pass the course. If students learn the required material and pass, then the
program can begin to consider itself as successful.
Conclusions
It is not within the scope
of this paper to solve the problems of remedial mathematics' low pass rate or
even to document the actual percentage improvement of variables in a college
mathematics classroom situation. All that has been within our purview is to
illustrate the process by which one urban university registered variable
success at bringing under prepared students into the regular college program of
studies. Nonetheless, the authors of this paper have no doubt that one of the
most important variables leading to substantial increase in skill
accomplishment was the Supplemental Instruction Program. At Downtown University,
student success in all classes with a peer tutor was significantly about 10%
higher than those without supplemental instruction (Getz, 2006a). The results
for the mathematics classes in particular are shown in Figures 1a and 1b.
For a time the Algebra
Tutorial pass rates were moving upward, but lately they have stalled and even
regressed so that the numbers in some ways just look as though they are merely
fluctuating. It seems that mathematics students need all the support services that
were provided by our Learners Community. Unfortunately, there has been a
reduction in the number of dollars available for remediation with the severely
reduced Title V funding of the parenting organization of the SI program - the
Learners Community. This has left the remedial program in mathematics and other
disciplines without the multipronged intervention system of the Learner's
Community, the Supplemental Instruction program, and Linked courses that
allowed the university to move upwards from 39% of 924 students passing in the
Fall 1998 semester to an overall passing average of 42% for 7377 students
through Fall 2005. Supplemental Instruction alone does not look sufficient to
produce statistically significant improvement in the pass rate for Algebra
Tutorial.
With the Fall data looking
different from the Spring results, perhaps detailed correlations should be
investigated. Further research, controlling for variables such as placement score,
might be illuminating. The Spring Algebra Tutorial classes mostly contain
students who have already failed the course at least once (Getz, 2006b). The
numbers tell "what" but not "why" students pass or fail to
pass Algebra Tutorial. The most recent statistics available concerning this
course make it painfully clear, even within the narrow scope of this work, that
more must be done to improve the pass rate in Algebra Tutorial.
One event probably did not
land a student in remedial mathematics coursework. It is unlikely that only one
form of intervention will cause a student success. A multipronged approach has
been successful and therefore preferable to any one-element approach. If only
one element is available, the most effective element is Supplemental Instruction.
In general, Downtown
University has
experienced a 10% pass rate increase in SI sections (Getz, 2006a). Currently the
university is contemplating extending the SI program to all sections of three
gatekeeper courses. Unfortunately, Algebra Tutorial is not one of those three.
With the present budgetary and societal conditions, other avenues must be
investigated to obtain another movement forward in the pass rate for Algebra
Tutorial.
References
Ainsworth,
L., Garnett, D., Phelps, D., Shannon, S., & Ripperger-Suhler, K.
(1994).
Steps in starting supplemental instruction. In D.Martin & D.
Arendale
(Eds.), Supplemental instruction: Increasing achievement and
retention.
New Directions for Teaching and Learning, 60(Winter), 23-29.
Arendale,
D. (1994). Understanding the supplemental instruction model. In D.
Martin
& D. Arendale (Eds.), Supplemental instruction: Increasing
achievement
and retention. New Directions for
Teaching and Learning, 60
(Winter),
11-21. San Francisco:
Jossey-Bass.
Arendale,
D. (1998). Increasing efficiency and effectiveness of learning for
freshman
students through supplemental instruction. In J. Higbee & P.
Dwinell
(Eds.), Developmental education:
Preparing successful college
students (Monograph
No. 24). Columbia, SC:
University of South
Carolina, National
Resource Center
for The First-Year Experience &
Students
in Transition.
Berliner,
D. (1990). The place of process-product research in developing the
Agenda
for research on teacher thinking. Educational
Psycho Linguist,
24(4),
325-344. Retrieved September 5, 2005, from Arizona State
University College of Education Web site
http://courses.ed.asu.edu/berliner/readings/process.htm
Betts, J.,
Zau, A., & Rice, L. (2003). Determinants
of student achievement: New
evidence
from San Diego.
San Francisco: Public
Policy Institute of
California. Retrieved
July 22, 2005, from Public Policy Institute of
California
Web site: http://www.ppic.org/content/pubs/R_803JBR.pdf
Boylan, H.
(1999). Exploring alternatives to remediation. Journal of
Developmental
Education, 22(3). Retrieved August 23, 2000 from
http://www.ncde.appstate.edu/reserve%20...22-3alternatives%20to%20remediation.htm
Boylan, H.,
& Saxon, D. (2000). What works in
remediation: Lessons from 30
years
of research. Prepared for: The League for Innovation
in
the Community College national Center for Developmental Education.
Retrieved
August 23, 2000, from
http://www.ncde.appstate.edu/reseerve%20reading/what%20works.htm
Breneman,
D., & Haarlow, W. (2002). Remedial education: Costs and
consequences.
In Remediation in higher education: A
symposium.
Washington, DC:
Thomas B. Fordham Foundation. Retrieved on
September
23, 2002, from http://www.edexcellence.net/library/remed.html
Burmeister,
S., Carter, J., Hockenger, L., Kenney, P., McLauren, A., & nIce, C.
(1994).
Supplemental instruction sessions in college algebra and
calculus.
New Directions for Teaching and Learning,
60(Winter), 53-61.
Davidson,
R., & Hanson, G. (2000). Information
for faculty members interested in
the
Downtown University supplemental instruction
program. Houston,
TX:
Downtown University,
University College memo.
Dewey, J.
(1916). Democracy and education: An
introduction to the philosophy of
education.
NY: The Free Press.
Downtown University. (1999). Key terms & definitions. Houston, TX: University College, Advising Center,
internal memorandum.
Downtown University. (2003a). Algebra Tutorial syllabus. Houston, TX:
Department
of Computer and Mathematical Scences, internal publication.
Downtown University. (2003b). Department policies and procedures. Houston,
TX:
Department of Computer and Mathematical Sciences, internal
publication.
Downtown University. (2005). Spring 2005semester: 20th day
preliminary
reports
FACT SHEET. Houston,
TX: Internal publication.
Finder, A.
(2006). Debate grows as colleges slip in graduations. Retrieved
September
18, 2006, from
http://www.nytimes.com/2006/09/15/education/15graduate.html
Gardner,
J., Barefoot, B., & Swing, R. (2001). Guidelines
for evaluating: The
first-year
experience at four-year colleges (2nd ed.). Columbia, SC:
University of South Carolina,
national Resource
Center for The First-Year
Experience
and Students in Transition.
Gersten,
G., Jordan, N., & Flojo, J. (2005). Early identification and interventions
for
students with mathematics difficulties. Journal
of Learning
Disabilities,
38(4), 293-304. Retrieved September 9, 2006, from
http://vnweb.hwwilson.com/hww/results/results_single_ftPES.jhtml
Getz, G.
(2006a). Report on the Learners
Community. Houston, TX: Downtown
University,
Learners Community internal memorandum.
Getz, G.
(2006b). Longitudinal data. Houston, TX: Downtown University,
internal
memorandum.
Good, T.,
Mulryan, C., & McCaslin, M. (1992). Grouping for instruction in
mathematics:
A call for programmatic research on small-group
processes.
In D. Grouws (Ed.), Handbook of research
on mathematics
teaching
and learning: A project of the National Council of Teachers of
Mathematics
(pp.165-196). New York:
Simon & Schuster Macmillan.
Greenberg,
J. (1999). How do we value teaching?: Voices of the students
[electronic
version]. The National Teaching and
Learning Forum, 8(2),
Retrieved
September 5, 2005, from
http://www.ntlf.com/html/lib/suppmst/82green.htm
Greenwald,
R., Hedges, L., & Laine, R. (1996). The effect of school resources
on
student achievement. Review of
Educational Research, 66(3), pp. 361-
396.
Retrieved July 22, 2005, from JSTOR Web site:
http://jstor.org.ezproxy.lib.uh.edu/jstor/gifcvtdir/ap002755/00346543/ap040307/04a...
Henscheid,
J. (Ed.). (2004). Integrating the
first-year experience: The role of
first-year
seminars in learning communities (Monograph No. 39).
Columbia, SC: University of South Carolina,
National Resource Center
for
the First-Year Experience & Students in Transition.
Higbee, J.,
& Dwinell, P. (1998). Transitions in developmental education at the
University of Georgia. In J. Higbee & P. Dwinell
(Eds.), Developmental
education:
Preparing successful college students (monograph No. 24).
Columbia, SC: University of South Carolina,
National Resource Center
for
The First-Year Experience & Students in Transition.
Judge, M. (2006). Supplemental
instruction program description and procedure.
Houston, TX: Downtown University, Learners Community, internal
report.
Kannapel, P.,
Clements, S., Taylor, D., & Hibpshman, T. (2005a). Characteristics
of
high-performing, high-poverty schools. Abstract retrieved March 16,
2005,
from ASCD Research Brief, 3(6) Web
site: http://www.ascd.org/portal/site/ascd/template.MAXIMIZE/menuitem.03e1753c019b7a9f9...
Kannapel,
P., Clements, S., Taylor, D., & Hibpshman, T. (2005b). Inside the black box of high-performing high-poverty schools. Retrieved
July 20,
2005,
from the Prichard Committee for Academic Excellence Web site:
http://www.prichardcommittee.org/Ford%20Study/FordReportJE.pdf
Kenney, P.,
& Kallison, J., Jr. (1994). Research studies on the effectiveness of
supplemental
instruction in mathematics. New
Directions for Teaching
and
Learning, 60(Winter), 75-82.
Kinach, B.
(1995). Grounded theory as scientific method: Haig-inspired
reflections
on educational research methodology. Retrieved September 5,
2005,
from
http://www.ed.uinc.edu/EPS/PES-Yearbook/95_docs/kinach.html
Lewis, L.
Farris, E., & Greene, B. (1997). Remedial
education at higher
education
institutes in fall 1995 (National
Center for Education
Statistics,
NCES
97-584). Washington, DC:
U. S.
Department of Education, Office
of
Educational Research and Improvement. Retrieved July 22, 2003, from
http://www.nces.ed.gov/surveys/peqis/publications/97584
Love, A.,
& Tokuno, K. (1999). Learning community models. In J. Leveine (Ed.),
Learning communities: New structures, new
partnerships for learning
(Monograph
No. 26). Columbia, SC:
University of South Carolina,
National Resource Center
for The First-Year Experience.
Mansfield, W., Farris, E., & Black, M.
(1991). College-level remedial education
in
the fall of 1989: Contractor report (National Center
for Education
Statistics,
NCES 91-191). Washington, DC:
U. S.
Department of
Education,
Office of Educational Research and Improvement. Retrieved
July
23, 2003 from http://www.nces.ed.gov/surveys/PEQIS/publications
Martin, D.,
& Arendale, D., (Eds.). (1994). Supplemental
instruction: Increasing
achievement
and retention. San
Francisco: Jossey-Bass.
Martin, D.,
& Blanc, D. (1994). VSI: A pathway to mastery and persistence. New
Directions
in Teaching and Learning, 60(Winter), 83-91.
National
Evaluation Systems. (2003a). Overview of
the TASP test. Retrieved
October
8, 2003, from http://www.thea.nesinc.com/fac_sec1.htm
Orton, R.
(1998). How can teacher reasoning be practical? [Electronic version].
Educational Theory, 48(2). Retrieved
September 5, 2005, from
http://www.ed.uinc.edu/EPS/Educational-Theory/Contents/1998_2.asp
PLATO.R [computer
software]. (2000). Bloomington,
MN: PLATOR Learning,
Inc.
Retrieved November 11, 2003, from http://www.plato.com
Redden, E.
(2006, October 6). Methods for teaching math. Retrieved October 7,
2006,
from http://insidehighered.com/news/2006/10/06/math
Rishel, T.
(1999). A handbook for mathematics
teaching assistants. New York:
MAA.
Robison, C.
(2006, September 24). Since deregulation, college tuition costs 39%
more
than 3 years ago. Houston
Chronicle, pp. A1, A24.
Rockwell,
S. (2006). Facilitating the fourth R: Resilience. Kappa Delta Pi
Record,
43(1), 14-19.
St. Clair, K.
(1999). A case against compulsory class attendance policies in higher
education.
Innovative Higher Education, 23(3),
171-180.
Thielemann,
J. (1999). The role of resistance as a
determinant of persistence for
Minority
college students: A logistic regression analysis of a theoretical
Model
of student persistence. Unpublished doctoral dissertation,
University of Houston, Texas.
Tinto, V.,
& Riemar, S. (2000). Learning
communities and the reconstruction of
remedial
education in higher education. (NCPI Report). Syracuse, NY:
Syracuse University,
National Center on Postsecondary Teaching,
Learning
and Assessment. Retrieved October 1, 2000 from
http://soeweb.syr.edu/hed/tinto/ncpi.htm
U. S. News
& World Repot. (2000). Online U. S.
news: College rankings.
Retrieved
September 1, 2000, from
http://www.usnews.com/usnews/edu/ugrad01/drank_12826.htm
Viadero, D.
(2004, July 14). "What Works" research site unveiled. Education
Week.
Retrieved April 25, 2005, from
http://www.kidsohio.org/headlines/archieve/20040714_EdWeek.htm
Viadero, D.
(2005, March 23). Math emerges as a big hurdle for teenagers: H. S.
improvement
hinges on 'critical' subject. Education
Week. Retrieved
March
28, 2005, from http://www.edweek.org/ew/articles/2005/03/23/28math.h24.html?rale=14RcsgF70mPtCaS...
Waller, W.
(2002, April). Report on best practices
in developmental math
courses.
Houston, TX:
Downtown University, Department of Computer
and
Mathematical Sciences, Pre-calculus Program Committee,
unpublished
report.
Waller, W.
(2003). Course statistics. Houston, TX: Downtown University,
Department
of Computer and Mathematical Sciences, internal
memorandum.
Waller, W.
(2005). Results. Houston,
TX: Downtown
University, Department of
Computer
and Mathematical Sciences, internal memorandum.
Widmar, G.
(1994). Supplemental instruction: From small beginnings to a
national
program. In D. Martin & D. Arendale (Eds.), Supplemental
instruction:
Increasing achievement and retention. New
Directions for
Teaching
and Learning, 60(Winter), 3-10. San Francisco, CA:
Jossey-
Bass.
_____________________________________________________________________
Table 1
Algebra Tutorial
Enrollment
_____________________________________________________________________ 1998
1999 2000 2001 2002 2003 2004
2005
2006
Fall 924 926 805 931 995 989 855 952
Spring
669 497 633 637 616
649 479
458
________________________________________________________________________
_______________________________________________________________________
Table 2
Pass
Rates for Algebra Tutorial Program
________________________________________________________________________
|
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
________________________________________________________________________
|
Fall
|
39%
|
43%
|
46%
|
42%
|
45%
|
43%
|
41%
|
35%
|
|
|
Spring
|
|
38%
|
33%
|
36%
|
31%
|
37%
|
35%
|
35%
|
31%
|
________________________________________________________________________